The Generalized Sliced-Wasserstein (GSW) distance is an extension of the popular Sliced-Wasserstein distance, used in comparing probability distributions. However, computing this distance can become computationally expensive, especially in high-dimensional settings. In this paper, we explore a fast approximation method for GSW, focusing on the key concepts, theoretical insights, and empirical findings.
The GSW distance is widely used in machine learning for applications like generative modeling, but its efficiency suffers when dealing with high-dimensional data. The motivation behind this paper is to propose fast and deterministic approximations for the GSW distance, particularly when the defining functions are polynomial functions or neural network-type functions. The paper seeks to reduce the complexity of the GSW approximation using these structured functions, providing a more scalable approach.
The Sliced-Wasserstein (SW) distance is typically computed by projecting the high-dimensional data into one dimension using random projections and calculating the Wasserstein distance between the projected distributions. The formula for the SW distance between two probability measures $\mu$ and $\nu$ is given by:
$$
SW_p(\mu, \nu) := \left( \int_{\mathbb{R}^d} W_p^p(\theta^* \# \mu, \theta^* \# \nu) d\gamma_d(\theta) \right)^{\frac{1}{p}},
$$
where $\theta^* \# \mu$ is the projection of the measure $\mu$ in the direction $\theta$.
The Generalized Sliced-Wasserstein (GSW) distance extends this by replacing the linear projection $\theta^*$ with a possibly non-linear function $g_\theta$, giving us:
$$
GSW_p(\mu, \nu) := \left( \int_{\mathbb{R}^d} W_p^p(g_\theta \# \mu, g_\theta \# \nu) d\gamma_d(\theta) \right)^{\frac{1}{p}},
$$
where $g_\theta$ could be any non-linear function, such as polynomial or neural network functions.
For a polynomial defining function, the GSW can be approximated with a multi-index $\alpha = (\alpha_1, \dots, \alpha_d) \in \mathbb{N}^d$ and a vector $x = (x_1, \dots, x_d) \in \mathbb{R}^d$. A polynomial function of degree $m$ is defined as:
$$
g_{\text{poly}}(x, \theta) := \sum_{|\alpha|=m} \theta_\alpha x^\alpha,
$$
where $\theta \in \mathbb{S}^{q-1}$ with $q = \binom{m+d-1}{d-1}$.
The following bound is derived for the approximation of the polynomial-GSW distance:
$$
\left| \text{poly-GSW}_2(\mu, \nu) – W_2(\eta_{\mu_q}, \eta_{\nu_q}) \right| \leq O(d^{-m/8}),
$$
where $\eta_{\mu_q}$ and $\eta_{\nu_q}$ are approximations of the original distributions $\mu_q$ and $\nu_q$.
The approximation for the polynomial GSW is given by:
$$
\text{poly-}\widehat{\text{GSW}}_2^2(\mu, \nu) = \text{poly-}\widehat{\text{GSW}}_2^2(\mu_q, \nu_q) + q^{-1} \|\widehat{m}_{\mu_q} – \widehat{m}_{\nu_q}\|^2,
$$where $\mu_q$ and $\nu_q$ are centered versions of the distributions $\mu$ and $\nu$.
For the neural network type function, the defining function is given by a composition of random matrices $\Theta$, each of size $d \times d$:
$$
g_{\text{neural}}(x, \theta) := \langle \theta, \Theta^{(1)} \dots \Theta^{(n)} x \rangle.
$$
For the neural network type functions, the approximation bound is:
$$
\left| \text{neural-GSW}_2(\mu, \nu) – W_2(\mu^*, \nu^*) \right| \leq O(3^{n/4} d^{-1/4} + d^{-1/8}).
$$
These bounds demonstrate the effectiveness of the proposed fast approximation methods, particularly in high-dimensional settings.
Under certain assumptions, the neural GSW distance approximation is:
$$
\text{neural-}\widehat{\text{GSW}}_2^2(\mu, \nu) = d^{-1} \left( \sqrt{\widehat{m}^2(\mu^*)} – \sqrt{\widehat{m}^2(\nu^*)} \right)^2,
$$
where $\mu^*$ and $\nu^*$ are the distributions transformed by the neural network projections.
The empirical evaluation of the proposed methods includes experiments with both polynomial and neural network defining functions. The results compare the fast approximations to the Monte Carlo GSW method, which uses a large number of projections.
The following results were obtained:
– Multivariate Gaussian Distributions: The fast approximations exhibit significantly lower approximation errors compared to the Monte Carlo method, especially as the number of projections increases.
– Gamma Distributions: Similar trends were observed for Gamma distributions, where the fast approximation provided competitive performance.
– Autoregressive Processes (AR(1)): The approximations also performed well when applied to autoregressive time series data, further validating the efficiency of the proposed methods.
Figures from the experiments demonstrate the approximation errors compared to the Monte Carlo GSW method:
Figure 1: Approximation Error for Gaussian and Gamma Distributions
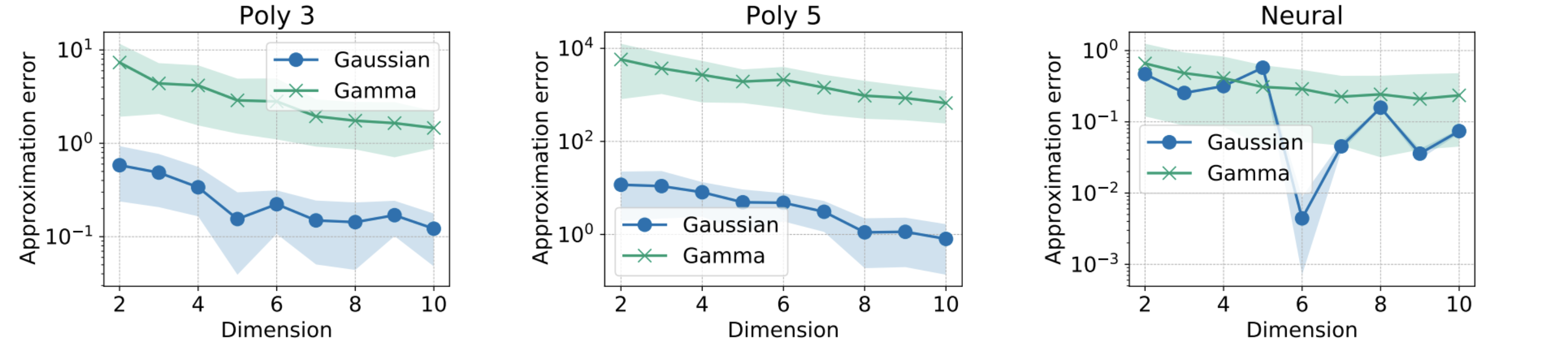
Figure 2: Approximation Error for AR(1) Processes
This paper introduces fast and deterministic methods for approximating the Generalized Sliced-Wasserstein distance using polynomial and neural network type functions. The theoretical guarantees, combined with empirical validation, show that these methods are highly efficient for high-dimensional data, offering significant computational savings without sacrificing accuracy.
Read our paper (ICASSP 2024) here!
Overall
Trang Nguyen*, Dung Le, Huy Nguyen, Khai Nguyen, Nhat Ho
Share Article
Hoang Ngo and Dat Quoc Nguyen
Hieu Trung Nguyen*, Duy Nguyen*, Khoa D. Doan, Viet Anh Nguyen
Thinh Pham, Dat Quoc Nguyen
VinAI Research, Vietnam
Thanh-Thien Le, Viet Dao, Linh Van Nguyen, Thi-Nhung Nguyen, Linh Ngo Van, Thien Huu Nguyen
