Trang Nguyen*, Dung Le, Huy Nguyen, Khai Nguyen, Nhat Ho
Counterfactual Plans under Distributional Ambiguity
Introduction
Machine learning models, thanks to their superior predictive performance, are blooming with increasing applications in consequential decision-making tasks such as loan approvals, university admission, job hiring, etc. Along with the potential to help make better decisions, current machine learning models are also raising concerns about their explainability and transparency, especially in domains where humans are at stake.
Consider a scenario where a student applying for a PhD program. She sends her profile which is a vector of covariate features which might include her age, undergrad score, GRE, and the number of publications to the university. However, she got a rejection by a machine learning model that are deployed by the university to filter applicants. She gets a rejection email and might ask further that “what can I do to get admitted?”.
Counterfactual explanation is emerging as a solution to answer these questions. A counterfactual explanation suggests how the input instance should be modified to alter the outcome of a predictive model. For example, such an explanation can be of the form “have one more publication in top-tier conferences” or “increase GRE by 15”. A pre-emptive design choice is to provide the nearest example to the input instance that flips model’s prediction to alleviate user’s effort in implementing these suggestions. However, in practice, providing one single example for every user having the same covariates may not be satisfactory since the covariates could barely capture user’s preferences to modify their input; thus, it is favorable to provide a “menu” of possible explanations and let the applicant choose one that fits them best. These set of explanations are called counterfactual plans (CFP).
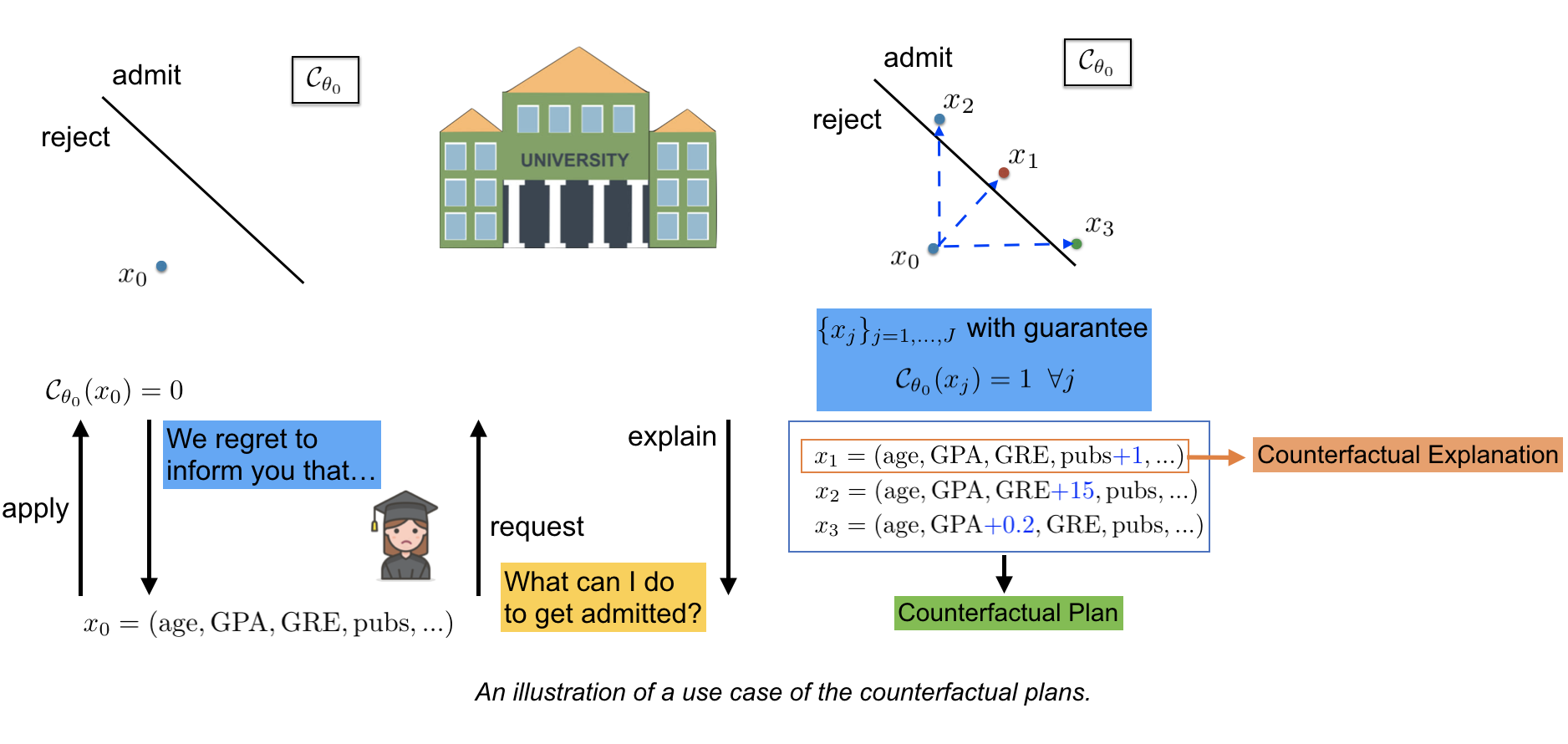
Constructing a counterfactual plan in the real world deployments requires to consider the several criteria:
- Effectiveness: each counterfactual should effectively reverse the unfavorable prediction of the model into a favorable one.
- Proximity: the counterfactuals should be close to the original input instance to alleviate the efforts required, and thus to encourage the adoption of the recourse.
- Diversity: the plan should also be diverse so that can capture different user’s preferences.
- Actionability: the counterfactual should suggests the actions that are “doable” somehow by the users. For example, it should not suggest the student to decrease their age.
Motivation
From the literature, there are several methods proposed to construct counterfactual plans including mixed integer programming (MIP) (Russel, 2019), multi-objective evolutionary algorithm (Dandl et al., 2020), iterative, gradient-based algorithm (Mothilal et al., 2020).
However, these methods often assume the classifier does not change over time and generate the counterfactual plans with respect to this classifier only. However, This assumption may not hold in practice, especially when involving human.
Suppose that the student received a CFP and decided to implement one of the explanations, says, “to publish another paper in a top-tier conference”. Because of taking time to implementing it, the student applies in the next year.
However, due the arrivals of new data or calibration of the old data, the university has updated their predictive model. The model’s parameter has been changed accordingly. The student gets a rejection again simply due to updates of the model, even though having the covariates similar to the explanation suggested in the last year. This indeed violates the promise and original spirit of the counterfactual explanations.
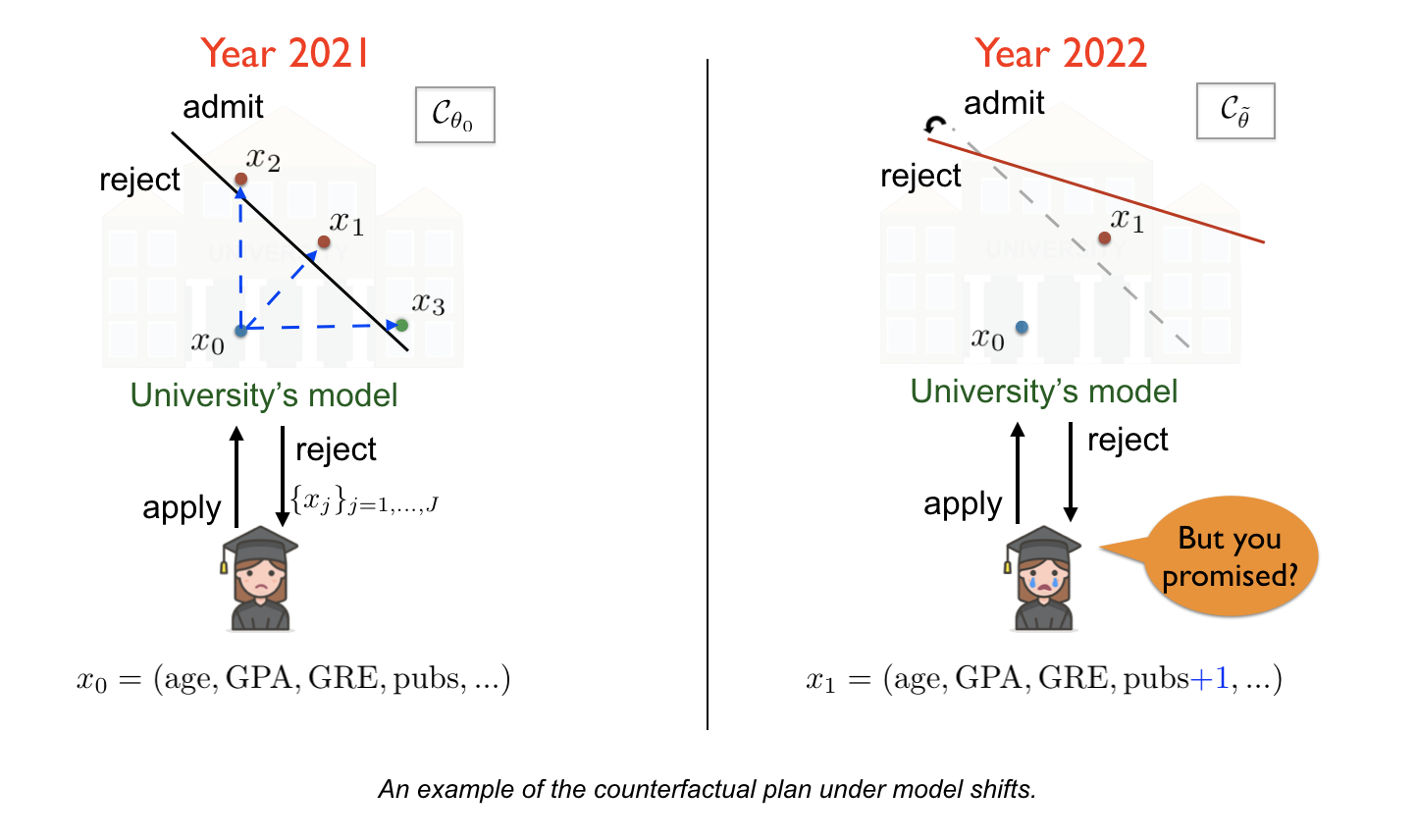
This example highlights the importance of taking the model’s uncertainty into account when we construct the counterfactual plan. Recently, Upadhyay et al. (2021) studied this problem and propose a minimax optimization inspired by adversarial training to generate a robust counterfactual explanation. However, this work focuses on the single counterfactual case only. Furthermore, this work considers all future model parameters in an uncertainty set (p-norm ball) equally important. That can lead to the counterfactual plan being overly conservative due to hedging against a pathological parameter.
Inspired of those, we study the problem of generating counterfactual plans and propose a probabilistic diagnostic tool to assess the the validity of CFPs under potential changes in model’s parameter.
Validity Quantifications
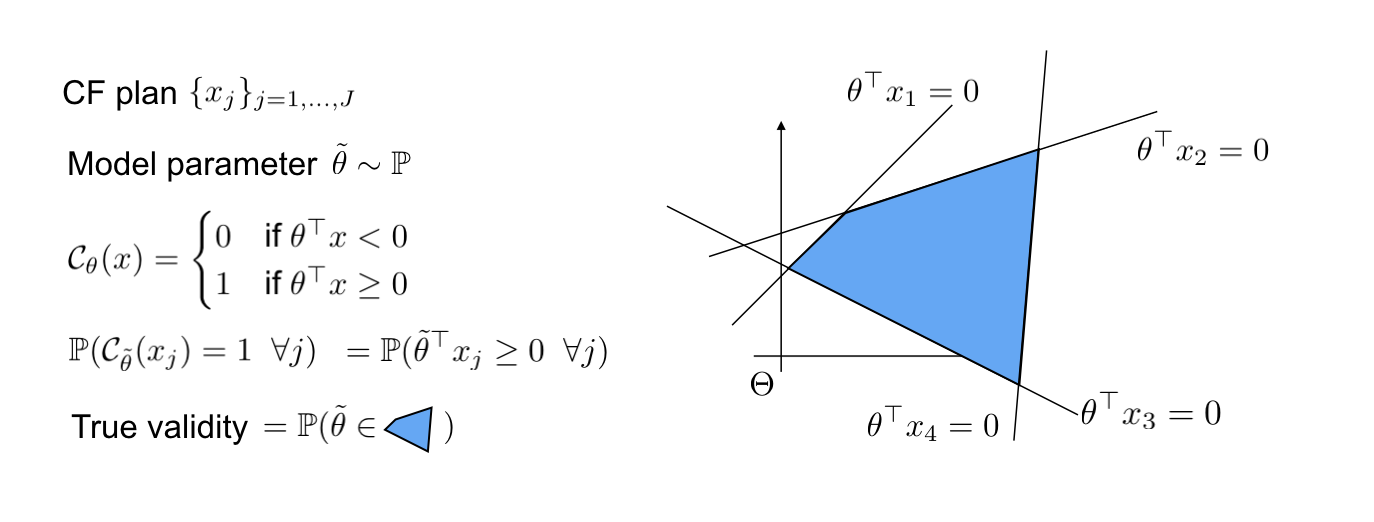
Given a binary classifier (1 denotes the favorable outcome and 0 is unfavorable) and a counterfactual plan, we consider this plan valid if every counterfactual in the plan is valid.

For each specific value of the model’s parameter, we can determine the feasibility of the plan by passing each counterfactual through the model. We then call the set of parameters that result in a valid plan as favorable parameter set.
Assume that the future parameter of the model is stochastic that follows an ambiguous distribution $mathbb{P}$. The validity of the plan is then characterized by the probability of the model’s parameter falling in the favorable parameter set.
In the case that the underlying classifier is a linear model, each counterfactual determines a hyperplane in the space of model’s parameter and a half-positive region of parameter that would yield a favorable outcome for this counterfactual. The favorable parameter set is then the intersection of the half-postive regions of all counterfactuals, which is a polyhedron as illustrated in the following example.
We suppose that the model parameter follows an ambiguous distribution $mathbb{P}$ belonging to the uncertainty set $mathbb{B}$, where $mathbb{B}$ is prescribed using a Gelbrich moment-based distance.

This ambiguity set $mathbb{B}$ is centered at a nominal distribution $hat{mathbb{P}}$ with known first and second moments. It contains every distribution that has the Gelbrich distance to the $hat{mathbb{P}}$ smaller than a predefined radius $rho$.
We are interested in finding the lower bound and upper bound of the true validity by taking the infimum and supremum operator for all distributions in the ambiguity set $mathbb{B}$. We then find out that we can compute the lower bound of the infimum and the upperbound of the supremum by solving linear semi-definite programming.
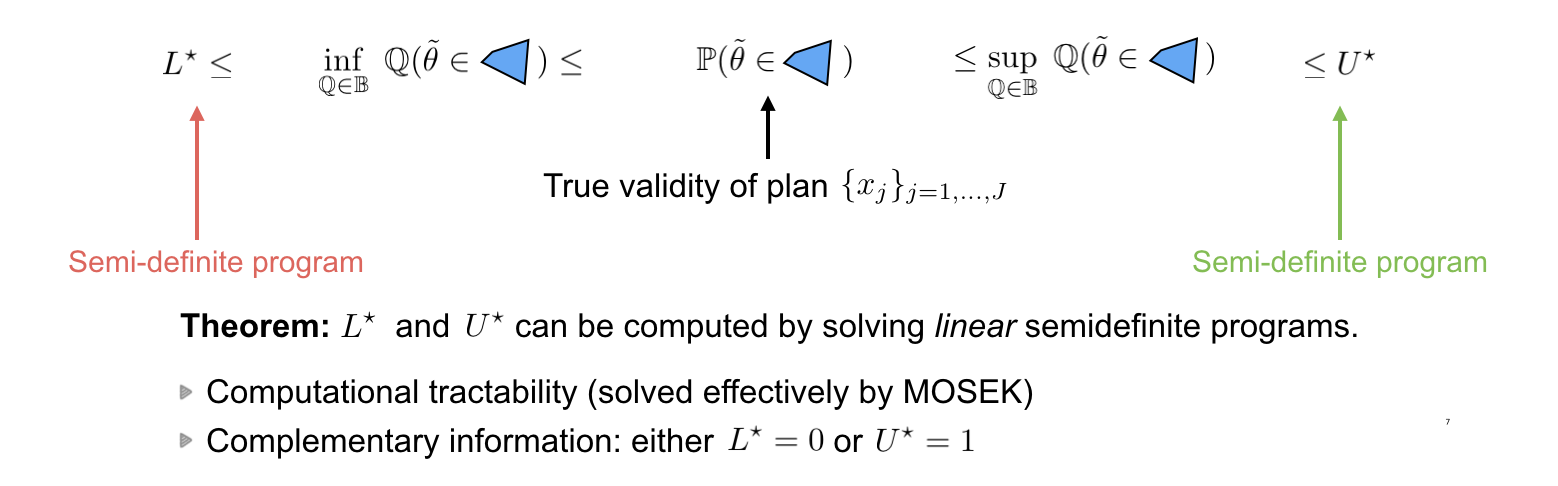
Because it is linear semi-definite program, it can be solved effectively using common solvers like MOSEK. Furthermore, we also find out that the lower bound and the upper bound are complementary information which literally says that in any case, either $L^star$ or $U^star$ is trivial.
Correction
Given a counterfactual plan, it may happen have low probability of being valid under random realizations of the future model parameter. The diagnostic tools in the pervious section indicate that a plan has low validity when the bounds are low, and we are here interested in correcting this plan such that the lower bound $L^star$ are increased.
We propose a heuristic method to improve the lower bound of the validity of the given plan. This heuristic leverages the solution of the lower bound semidefinite program and modifies the counterfactuals to increase the value of the lower bound.
Our correction procedure aims to modify each counterfactual in the way that maximizes the Mahalanobis distance from mean of the nominal distribution toward the hyperplane characterized by the counterfactual.
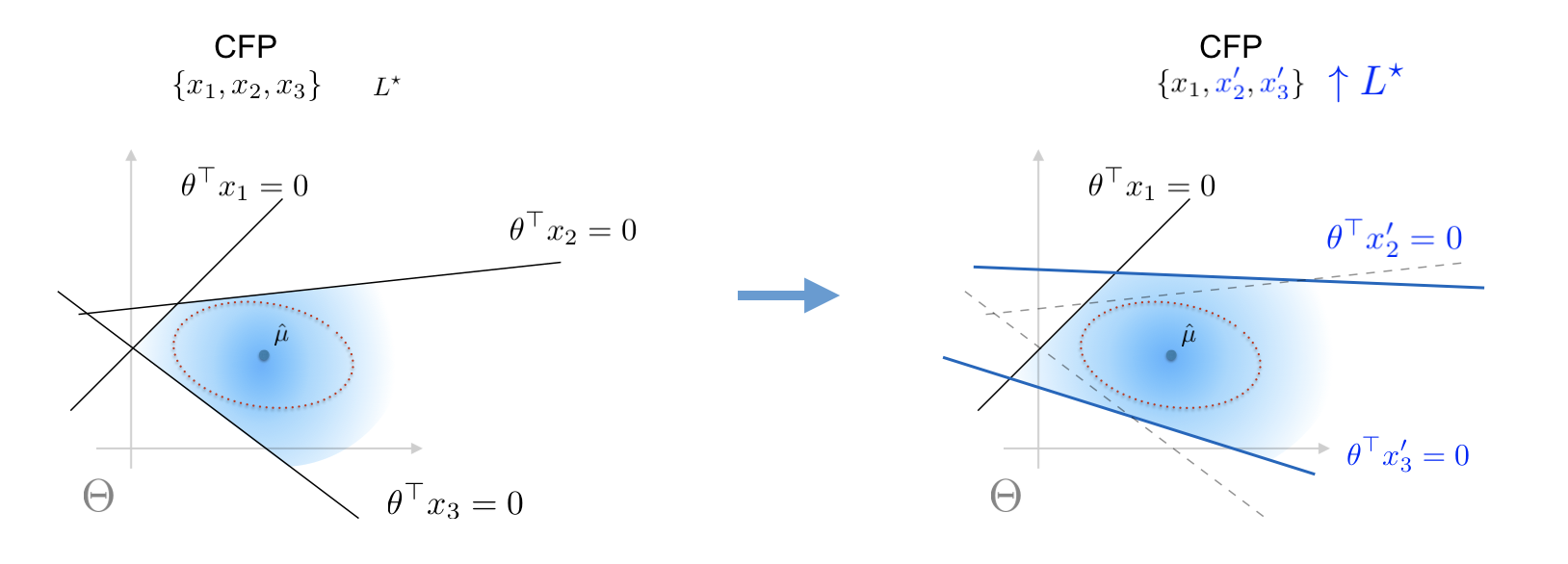
Construction
In order to construct the counterfactual plan from scratch, we propose an optimization problem in which the objective is a weighted sum of three terms:
- Proximity: Proximity is the average cost of adopting recommended changes, in this work, we use $ell_1$ distance to measure the difference between the counterfactual and the input instance.
- FutureValidity: we take the uncertainty of the future model parameter into consideration when estimating the validity of the plan. The future validity is the radius of maximum-volume ellipsoid that is centered at $hat{mu}$ and lies inside the set of favorable parameters.
- Diversity: Diversity is measured by the determinant of the similarity matrix, which contains the pairwise similarity between the elements in the plan.
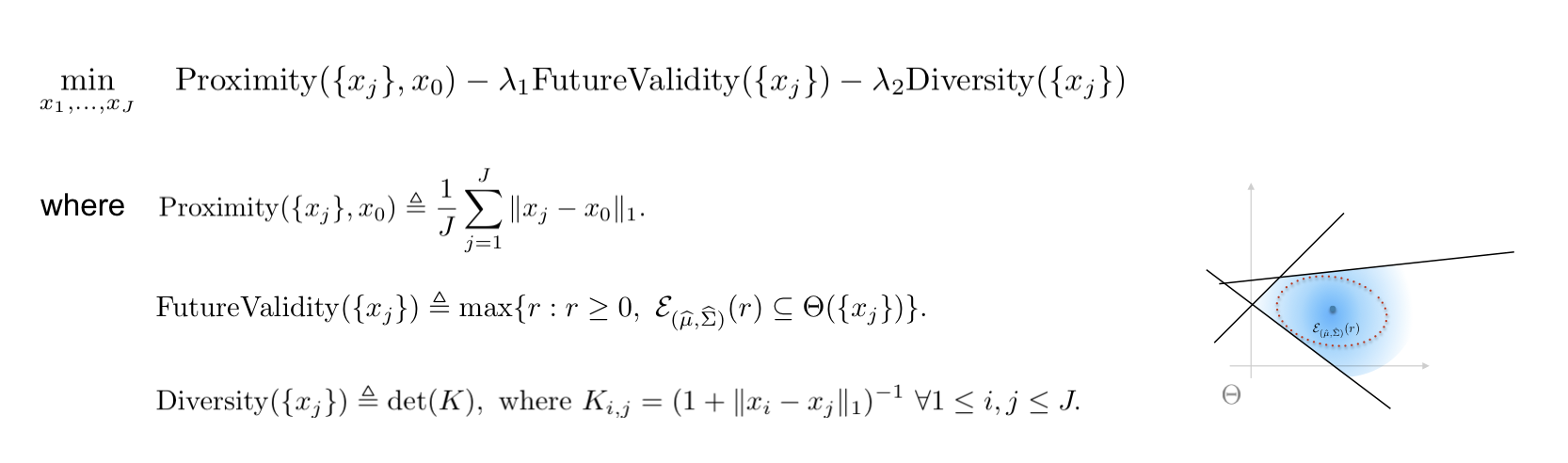
This problem can be solved by a projected gradient descent algorithm.
Empirical Results
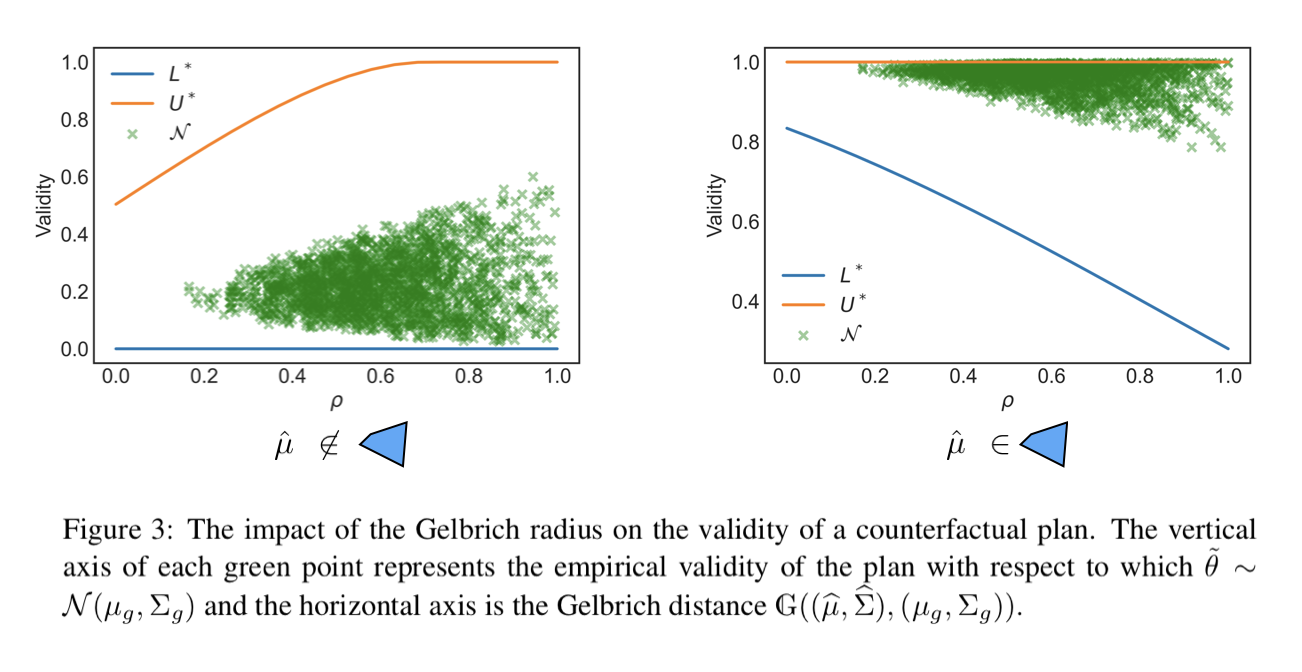
We conduct an experiment on synthetic data to validate our theoretical bounds. We fix a counterfactual plan, and fix the ambiguity set. We set $hat{mu}$ to $theta_0$ and $hat{Sigma}$ to $0.5 times I$. We then evaluate the lower bound and upper bound with different radius rho.
We also simulate different realizations of the parameters and evaluate the empirical validity. Each green dot is the validity of the plan with respect to a realization. For each realization, we sample tilde theta in a normal distribution, the mean and covariance of the normal distribution is chosen at random.
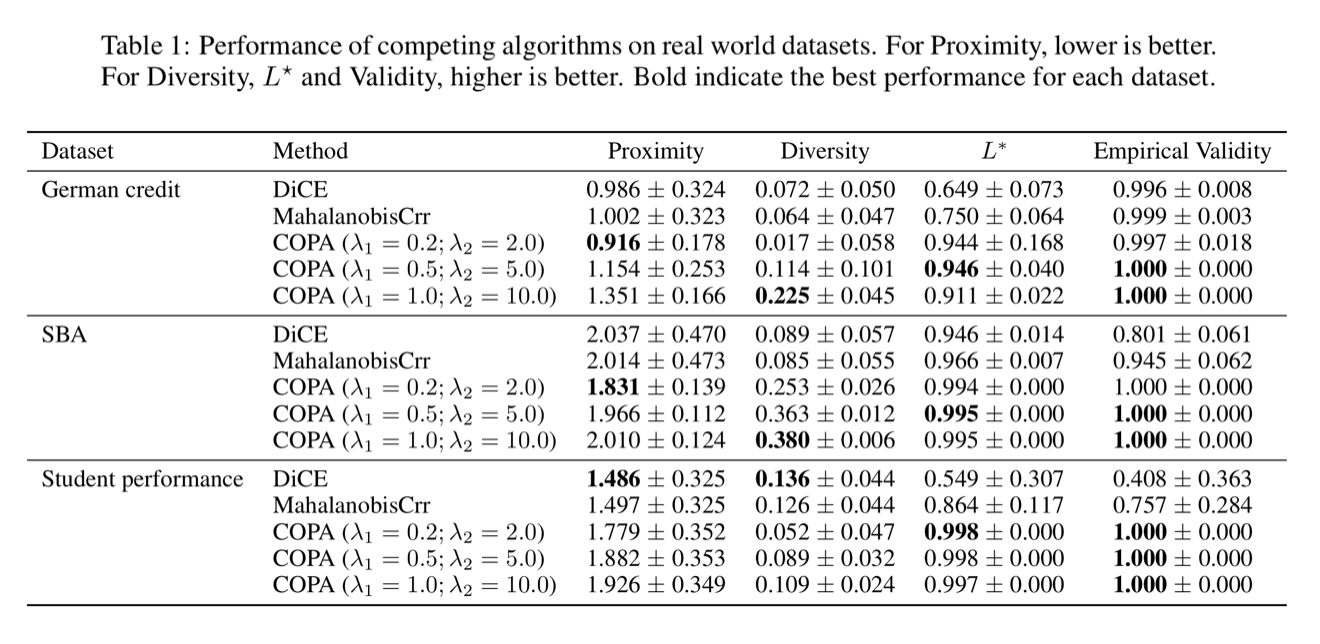
On the real-world datasets, we compare our method to a common method in generating CFPs to demonstrate the effectiveness of our methods. We have three datasets, each has two separate sets of data, one for the present data that used to train the current classifier. We will generate counterfactuals with respect to this classifier. We then use future data to train different future classifiers and use them to compute the empirical validity. The results comparing to DiCE show that our methods increase both lower bound and empirical validity with an acceptable trade-off in proximity.
Conclusion
In this work, we study the problem of generating counterfactual plans under the distributional shift of the classifier’s parameters given the fact that the classification model is usually updated upon the arrival of new data. We propose an uncertainty quantification tool to compute the bounds of the probability of validity for a given counterfactual plan, subject to uncertain model parameters. Further, we introduce a correction tool to increase the validity of the given plan. We also propose a COPA framework to construct a counterfactual plan by taking the model uncertainty into consideration. The experiments demonstrate the efficiency of our methods on both synthetic and real-world datasets. For further information, please refer to our work at https://arxiv.org/abs/2201.12487 .
References
Russell, Chris. “Efficient search for diverse coherent explanations.” Proceedings of the Conference on Fairness, Accountability, and Transparency. 2019.
Dandl, Susanne, et al. “Multi-objective counterfactual explanations.” International Conference on Parallel Problem Solving from Nature. Springer, Cham, 2020.
Mothilal, Ramaravind K., Amit Sharma, and Chenhao Tan. “Explaining machine learning classifiers through diverse counterfactual explanations.” Proceedings of the 2020 Conference on Fairness, Accountability, and Transparency. 2020.
Upadhyay, Sohini, Shalmali Joshi, and Himabindu Lakkaraju. “Towards robust and reliable algorithmic recourse.” Advances in Neural Information Processing Systems 34 (2021).
Overall
Ngoc Bui & Duy Nguyen (Research Resident), and Viet Anh Nguyen (Research Scientist)
Share Article




