GenAI

On Transportation of Mini-batches: A Hierarchical Approach

September 24, 2022

1. Introduction

The Optimal Transport (OT) theory has a long history in Applied mathematics and economics, and recently it has become a useful tool in machine learning applications such as deep generative models [1], domain adaptation [2], etc. Despite its popularity in ML, there are still major issues of computation cost with using OT in large-scale datasets, those issues could be demonstrated in two following situations: “What if the number of supports is very large, for example millions?” and “What if the computation of optimal transport is repeated multiple times and has limited memory e.g., in deep learning?”. To deal with those problems, practitioners often replace the original large-scale computation of OT with cheaper computation on subsets of the whole dataset, which is widely referred to as mini-batch approaches [3, 4]. In particular, a min-batch is a sparse representation of the data. Despite being applied successfully, the current mini-batch OT loss does not consider the relationship between mini-batches and treats every pair of mini-batches the same. This causes undesirable effects in measuring the discrepancy between probability measures. First, the m-OT loss is shown to be an approximation of a discrepancy (the population m-OT) that does not preserve the metricity property, namely, this discrepancy is always positive even when two probability measures are identical. Second, it is also unclear whether this discrepancy achieves the minimum value when the two probability measures are the same. That naturally raises the question of whether we could propose a better mini-batch scheme to sort out these issues to improve the performance of the OT in applications.

2. Background

2.1 Optimal Transport

Let $\mu, \nu$ be discrete distributions of $n$ supports, i.e. $\mu \coloneqq \frac{1}{n} \sum_{i=1}^n \delta_{x_i}$ and $\nu \coloneqq \frac{1}{n}\sum_{j=1}^{n} \delta_{y_j}$ . Given distances between supports of two distributions as a matrix $C$ , the Optimal Transport (OT) problem reads:

(1) $\begin{equation*} \text{OT}(\mu, \nu) = \min_{\pi \in \Pi(\mu, \nu)} \langle C,\pi \rangle \end{equation*}$

where $\Pi(\mu, \nu) = \{ \pi \in \mathbb{R}_{+}^{n \times n} | \pi 1 = \mu, \pi^T 1 = \nu \}$ is the set of admissible transportation plans between $\mu$ and $\nu$ .

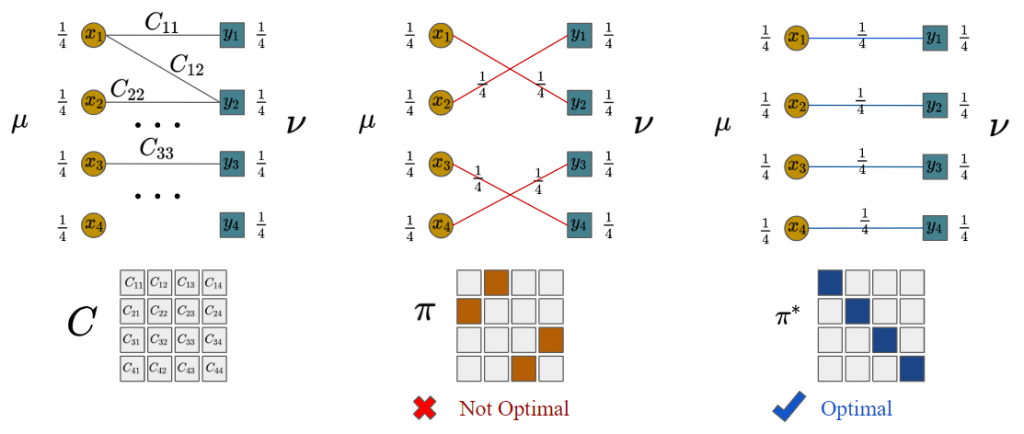
Figure 1. An example of OT with n = 4.

2.2 Mini-batch Optimal Transport

The original $n$ samples are divided into random mini-batches of size $m \geq 1$ , then an alternative solution to the original OT problem is formed by averaging these smaller OT solutions.

(2) $\begin{equation*} \text{m-OT}^m(\mu, \nu) = \mathbb{E}_{(X, Y) \sim \overset{\otimes m}{\mu} \otimes \overset{\otimes m}{\nu}} [\text{OT}(P_X, P_Y)] \end{equation*}$

where $\otimes$ denotes product measure, $X = (x_1, \ldots, x_m)$ is the sampled mini-batch, and $P_X = \frac{1}{m} \sum_{i=1}^m \delta_{x_i}$ is the corresponding discrete distribution. In practice, we can use subsampling to approximate the expectation, thus the empirical m-OT reads:

(3) $\begin{equation*} \text{m-OT}_k^m(\mu, \nu) \approx \frac{1}{k} \sum_{i=1}^k [\text{OT}(P_{X_i}, P_{Y_i})] \end{equation*}$

where $(X_1, Y_1), \ldots, (X_k, Y_k) \sim \overset{\otimes m}{\mu} \otimes \overset{\otimes m}{\nu}$ and $k$ is often set to 1 in previous works.

Issue of m-OT

We can see that the optimal matchings at the mini-batch level in Figure 2 are different from the full-scale optimal transport. One source of the issue is that all pairs of mini-batches are treated the same.

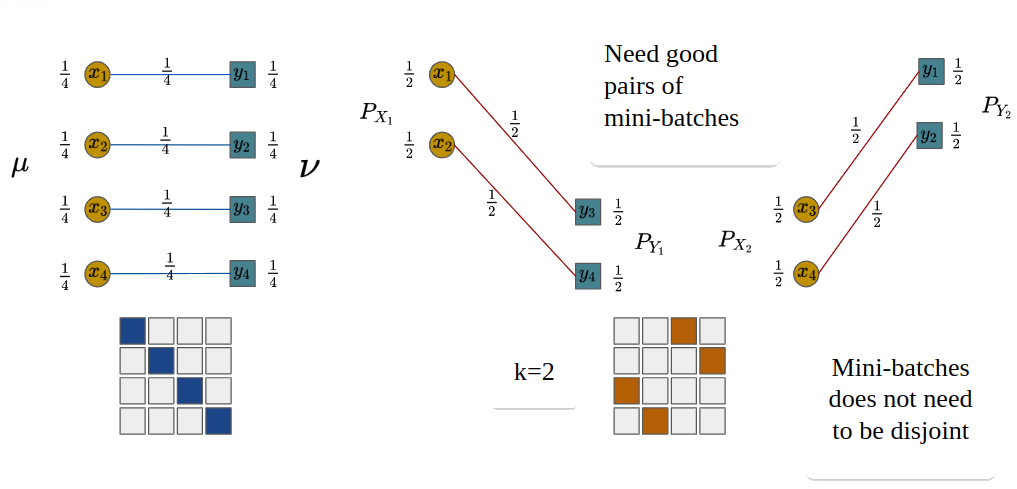
Figure 2. An example of m-OT with n = 4, m = 2 and k = 2.

3. Batch of Mini-batches Optimal Transport

To address the issues of m-OT, we solve an additional OT problem between mini-batches to find an optimal weighting for combining local mini-batch losses.

(4) $\begin{equation*} \text{BoMb-OT}^m(\mu, \nu) = \inf_{\gamma \in \Gamma(\overset{\otimes m}{\mu} \otimes \overset{\otimes m}{\nu})} \mathbb{E}_{(X, Y) \sim \gamma} [\text{OT}(P_X, P_Y)] \end{equation*}$

(5) $\begin{equation*} \text{BoMb-OT}_k^m(\mu, \nu) \approx \inf_{\gamma \in \Gamma(\overset{\otimes m}{\mu_k} \otimes \overset{\otimes m}{\nu_k})} \sum_{i=1}^k \sum_{j=1}^k \gamma_{ij}[\text{OT}(P_{X_i}, P_{Y_j})] \end{equation*}$

where $X_1, \ldots, X_k \sim \overset{\otimes m}{\mu}$ and $\overset{\otimes m}{\mu_k} = \frac{1}{k} \sum_{i=1}^k \delta_{X_i}$ . $Y_j (1 \leq j \leq k)$ and $\overset{\otimes m}{\nu_k}$ are defined similarly.

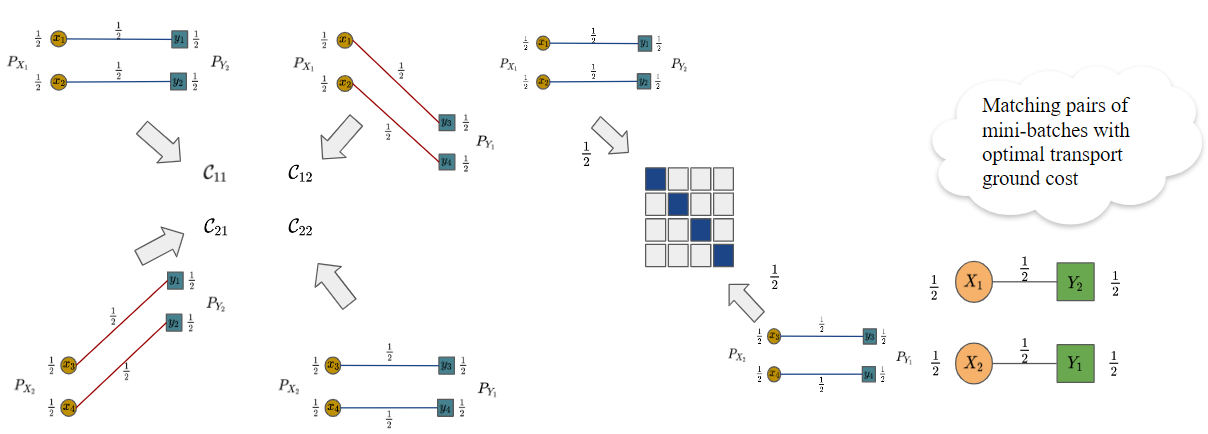
Figure 3. An example of BoMb-OT with n = 4, m = 2 and k = 2. After solving the OT problem between mini-batches, $X_1$ is mapped to $Y_2$ and $X_2$ is mapped to $Y_1$ , which results in the same solution as the full-scale optimal transport.

Training deep networks with BoMb-OT loss

In the deep learning context, the supports are usually parameterized by neural networks. In addition, the gradient of neural networks is accumulated from each pair of mini-batches and only one pair of mini-batches are used in memory at a time. Since the computations on pairs of mini-batches are independent, we can use multiple devices to compute them. We propose a three-step algorithm to train neural networks with BoMb-OT loss as follows.

4. Experiments

BoMb-(U)OT shows a favorable performance compared to m-(U)OT on three types of applications, namely, gradient-based (e.g., deep generative model, deep domain adaptation (DA)), mapping-based (e.g., color transfer), and value-based (e.g., approximate Bayesian computation (ABC)).

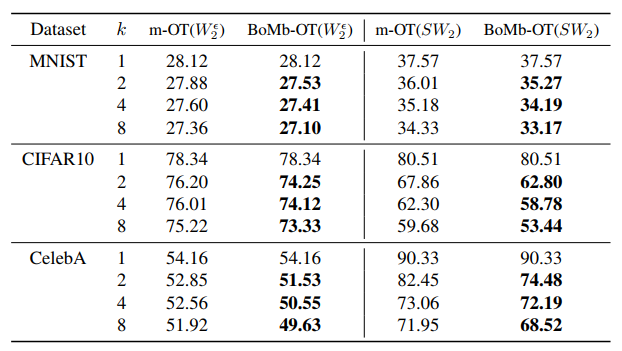
Table 1. Comparison between the BoMb-OT and the m-OT on deep generative models. On the MNIST dataset, we evaluate the performances of generators by computing approximated Wasserstein-2 while we use the FID score on CIFAR10 and CelebA.

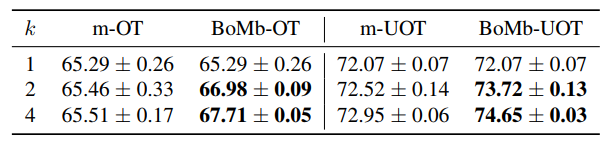
Table 2. Comparison between two mini-batch schemes on the deep domain adaptation on the VisDA dataset. We varied the number of mini-batches k and reported the classification accuracy on the target domain.

Figure 4. Experimental results on color transfer for full OT, the m-OT, and the BoMb-OT on natural images with (k; m) = (10; 10). Color palettes are shown under corresponding images.

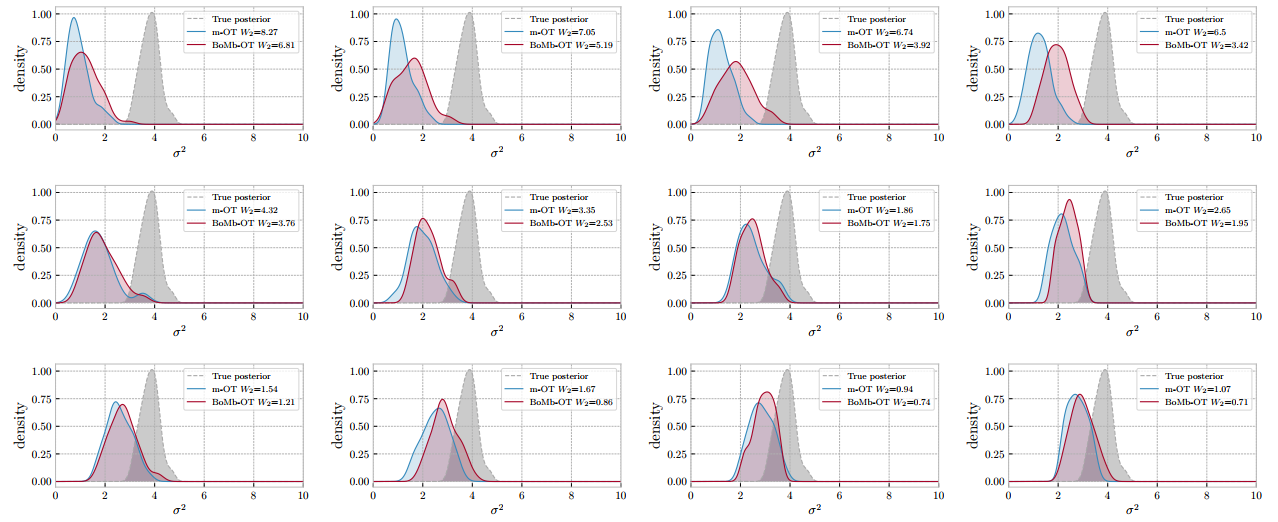
Figure 5. Approximated posteriors from ABC with the m-OT and the BoMb-OT. The first row, the second row, and the last row have m = 8, m = 16, and m = 32, respectively. In each row, the number of mini-batches k is 2; 4; 6; and 8 from left to right.

5. Conclusion

In this paper, we have presented a novel mini-batch method for optimal transport, named Batch of Mini-batches Optimal Transport (BoMb-OT). The idea of the BoMb-OT is to consider the optimal transport problem on the space of mini-batches with an OT-types ground metric. More importantly, we have shown that the BoMb-OT can be implemented efficiently and they have more favorable performance than the m-OT in various applications of optimal transport including deep generative models, deep domain adaptation, color transfer, approximate Bayesian computation, and gradient flow. For future work, we could consider a hierarchical approach version of optimal transport between incomparable spaces. For further information, please refer to our work at https://proceedings.mlr.press/v162/nguyen22d/nguyen22d.pdf.

References

[1] Arjovsky, M., Chintala, S., and Bottou, L. Wasserstein generative adversarial networks. In International Conference on Machine Learning, pp. 214–223, 2017.
[2] Courty, N., Flamary, R., Tuia, D., and Rakotomamonjy, A. Optimal transport for domain adaptation. IEEE transactions on pattern analysis and machine intelligence, 39(9):1853–1865, 2016.
[3] Fatras, K., Zine, Y., Flamary, R., Gribonval, R., and Courty, N. Learning with minibatch Wasserstein: asymptotic and gradient properties. In AISTATS 2020-23nd International Conference on Artificial Intelligence and Statistics, volume 108, pp. 1–20, 2020.
[4] Fatras, K., Zine, Y., Majewski, S., Flamary, R., Gribonval, R., and Courty, N. Minibatch optimal transport distances; analysis and applications. arXiv preprint arXiv:2101.01792, 2021b.

Robust Bayesian Recourse Read Now

VinAI released a training course used in its AI Residency Program: Linear Algebra Read Now

Back to Technical Blog

Overall

6 minutes

Dang Nguyen – Research Resident