Fast Approximation of the Generalized Sliced-Wasserstein Distance

The Generalized Sliced-Wasserstein (GSW) distance is an extension of the popular Sliced-Wasserstein distance, used in comparing probability distributions. However, computing this distance can become computationally expensive, especially in high-dimensional settings. In this paper, we explore a fast approximation method for GSW, focusing on the key concepts, theoretical insights, and empirical findings.

Motivations

The GSW distance is widely used in machine learning for applications like generative modeling, but its efficiency suffers when dealing with high-dimensional data. The motivation behind this paper is to propose fast and deterministic approximations for the GSW distance, particularly when the defining functions are polynomial functions or neural network-type functions. The paper seeks to reduce the complexity of the GSW approximation using these structured functions, providing a more scalable approach.

Backgrounds

The Sliced-Wasserstein (SW) distance is typically computed by projecting the high-dimensional data into one dimension using random projections and calculating the Wasserstein distance between the projected distributions. The formula for the SW distance between two probability measures and is given by:

SWp,  ≔  RdWpp* # , * #  dd  1p,

where *# is the projection of the measure in the direction .

The Generalized Sliced-Wasserstein (GSW) distance extends this by replacing the linear projection * with a possibly non-linear function g, giving us:

GSWp,≔RdWppg#,g#dd1p,

where g could be any non-linear function, such as polynomial or neural network functions.

Theoretical Results

Polynomial Defining Function

For a polynomial defining function, the GSW can be approximated with a multi-index \alpha=1,,dNd and a vector x=x1,,xdRd. A polynomial function of degree m is defined as:

gpolyx,≔=mx,

where Sq-1withq=m+d-1d-1.

The following bound is derived for the approximation of the polynomial-GSW distance:

poly-GSW2,–W2q,qOd-m/8,

where q andq are approximations of the original distributions q and q.

The approximation for the polynomial GSW is given by:

poly-GSW22,=poly-GSW22q,q+q-1|mq–mq|2,

where q and q are centered versions of the distributions and .

Neural Network Type Function

For the neural network type function, the defining function is given by a composition of random matrices , each of size dd:

gneuralx,≔⟨,1nx⟩.

For the neural network type functions, the approximation bound is:

neural-GSW2,–W2*,*O3n/4d-1/4+d-1/8.

These bounds demonstrate the effectiveness of the proposed fast approximation methods, particularly in high-dimensional settings.

Under certain assumptions, the neural GSW distance approximation is:

neural-GSW22,=d-1m2*–m2*2,

where * and * are the distributions transformed by the neural network projections.

Empirical Evaluation

The empirical evaluation of the proposed methods includes experiments with both polynomial and neural network defining functions. The results compare the fast approximations to the Monte Carlo GSW method, which uses a large number of projections.

The following results were obtained:

– Multivariate Gaussian Distributions: The fast approximations exhibit significantly lower approximation errors compared to the Monte Carlo method, especially as the number of projections increases.

– Gamma Distributions: Similar trends were observed for Gamma distributions, where the fast approximation provided competitive performance.

– Autoregressive Processes (AR(1)): The approximations also performed well when applied to autoregressive time series data, further validating the efficiency of the proposed methods.

Figures from the experiments demonstrate the approximation errors compared to the Monte Carlo GSW method:

Figure 1: Approximation Error for Gaussian and Gamma Distributions

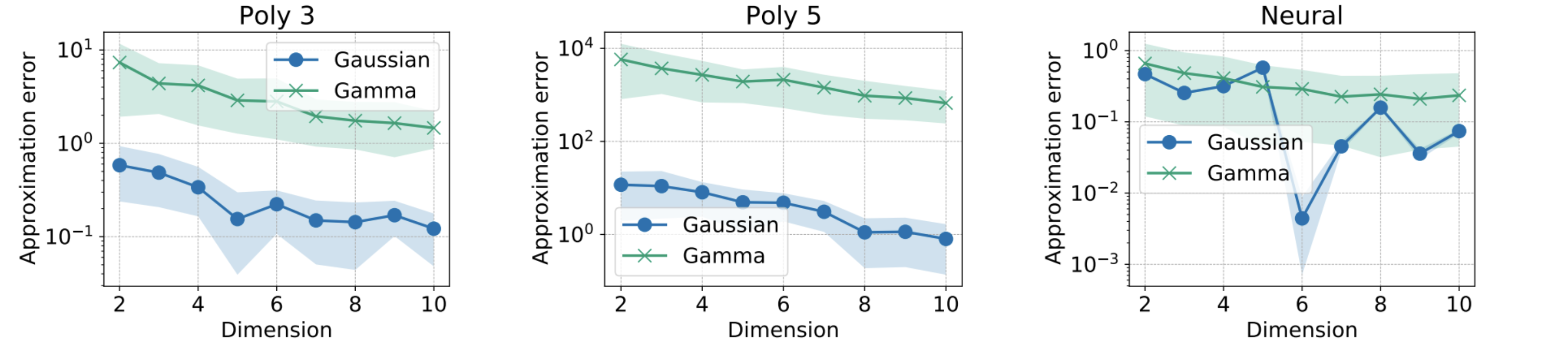
Figure 2: Approximation Error for AR(1) Processes

Conclusion

This paper introduces fast and deterministic methods for approximating the Generalized Sliced-Wasserstein distance using polynomial and neural network type functions. The theoretical guarantees, combined with empirical validation, show that these methods are highly efficient for high-dimensional data, offering significant computational savings without sacrificing accuracy.

Read our paper (ICASSP 2024) here! 

References

1. Bonneel, Nicolas, Julien Rabin, Gabriel Peyré, and Marco Cuturi. “Sliced and Radon Wasserstein barycenters of measures.” Journal of Mathematical Imaging and Vision 51, no. 1 (2015): 22-45.
2. Kolouri, Soheil, Gustavo K. Rohde, and Heiko Hoffmann. “Sliced-Wasserstein distance: A fast and differentiable approximation of the Earth Mover’s distance.” In Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 627-635. 2017.
3. Diaconis, Persi, and David Freedman. “Asymptotics of graphical projection pursuit.” The Annals of Statistics 12, no. 3 (1984): 793-815.
4. Nadjahi, Kimia, Alain Durmus, Pierre E. Jacob, Roland Badeau, and Umut Simsekli. “Fast approximation of the sliced-Wasserstein distance using concentration of random projections.” Advances in Neural Information Processing Systems 34 (2021): 12411-12424.