GenAI

Self-Attention Amortized Distributional Projection Optimization for Sliced Wasserstein Point-Cloud Reconstruction

July 31, 2023

1. Introduction

Based on the closed-form solution of Wasserstein distance in one dimension, Sliced Wasserstein (SW) has been utilized successfully in point-cloud representation learning [1, 2] due to its computational efficiency. However, the downside of SW is that it treats all projections the same due to the usage of a uniform distribution over projecting directions. Thus, max sliced Wasserstein (Max-SW) [3] distance was proposed as a solution for less discriminative projections of sliced Wasserstein (SW) distance. In applications that have various independent pairs of probability measures, amortized projection optimization [4] was introduced to predict the “max” projecting directions given two input measures instead of using projected gradient ascent multiple times. Despite being efficient, Max-SW and its amortized version cannot guarantee metricity property due to the sub-optimality of the projected gradient ascent and the amortization gap. Therefore, in this paper, we propose to replace Max-SW with distributional sliced Wasserstein distance with von Mises-Fisher (vMF) projecting distribution (v-DSW). Since v-DSW is a metric with any non-degenerate vMF distribution, its amortized version can guarantee the metricity when performing amortization. Furthermore, current amortized models are not permutation invariant and symmetric, thus they are not suitable to deal with set-based data (e.g. point-clouds). To address the issue, we design amortized models based on self-attention architecture. In particular, we adopt efficient self-attention architectures to make the computation linear in the number of supports. With the two improvements, we derive self-attention amortized distributional projection optimization and show its appealing performance in point-cloud reconstruction and its downstream applications.

2. Background

2.1 Optimal Transport

We denote a point-cloud of $m$ points $x_1,\ldots,x_m \in \mathbb{R}^d$ ( $d \geq 1$ ) as $X=(x_1,\ldots,x_m) \in \mathbb{R}^{dm}$ which is a vector of a concatenation of all points in the point-cloud. We denote the set of all possible point-clouds as $\mathcal{X} \subset \mathbb{R}^{dm}$ . In the point-cloud representation learning, we want to estimate $f_\phi:\mathcal{X} \to \mathcal{Z}$ ( $\phi \in \Phi$ ) jointly with a function $g_\gamma:\mathcal{Z} \to \mathcal{X}$ ( $\gamma \in \Gamma$ ) given a point-cloud dataset $p(X)$ (distribution over set of poin-clouds $\mathcal{X}$ ) by minimizing the objective:

(1) $\begin{equation*} \min_{\phi \in \Phi, \gamma \in \Gamma} \mathbb{E}_{X \sim p(X)} \mathcal{D}(X,g_\gamma (f_\phi(X))). \end{equation*}$

Here, $\mathcal{D}$ is a metric between two point-clouds.

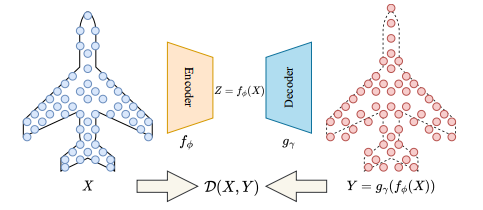
Figure 1. Overview of Point-cloud Reconstruction.

2.2 Max Sliced Wasserstein Distance

Max sliced Wasserstein (Max-SW) distance between $\mu \in \mathcal{P}_p(\mathbb{R}^d)$ and $\nu\in \mathcal{P}_p(\mathbb{R}^d)$ is:

(2) $\begin{equation*} \text{Max-SW}_p(\mu,\nu) = \max_{\theta \in \mathbb{S}^{d - 1}} W_p(\theta\sharp \mu,\theta \sharp \nu), \end{equation*}$

where the Wasserstein distance has a closed form on one dimension which is

(3) $\begin{equation*} W_p(\mu,\nu) = \left( \int_0^1 |F_\mu^{-1}(z) - F_{\nu}^{-1}(z)|^{p} dz \right)^{1/p}, \end{equation*}$

with $F^{-1}_{\mu}$ and $F^{-1}_{\nu}$ are the inverse CDF of $\mu$ and $\nu$ respectively.

Max sliced point-cloud reconstruction: Instead of solving all optimization problems independently, an amortized model is trained to predict optimal solutions to all problems. Given a parametric function $a_\psi: \mathcal{X}\times \mathcal{X} \to \mathbb{S}^{d-1}$ ( $\psi \in \Psi$ ), the amortized objective is:

(4) $\begin{equation*} \min_{\phi \in \Phi,\gamma \in \Gamma }\mathbb{E} \left[\max_{\theta \in \mathbb{S}^{d-1}}W_p(\theta \sharp P_X,\theta \sharp P_{g_\gamma (f_\phi(X))})\right], \end{equation*}$

the one-dimensional Wasserstein between two projected point-clouds can be solved with the time complexity $\mathcal{O}(m\log m)$ .

2.3 Amortized Projection Optimization

Instead of solving all optimization problems independently, an amortized model is trained to predict optimal solutions to all problems. Given a parametric function $a_\psi: \mathcal{X}\times \mathcal{X} \to \mathbb{S}^{d-1}$ ( $\psi \in \Psi$ ), the amortized objective is:

(5) $\begin{equation*} \min_{\phi \in \Phi,\gamma \in \Gamma}\max_{ \psi \in \Psi}\mathbb{E}_{X \sim p(X)}[W_p(\theta_{\psi,\gamma,\phi}\sharp P_X,\theta_{\psi,\gamma,\phi} \sharp P_{g_\gamma (f_\phi(X))})], \end{equation*}$

where $\theta_{\psi,\gamma,\phi} = a_\psi(X,g_\gamma (f_\phi(X)))$ .

3. Self-Attention Amortized Distributional Projection Optimization

3.1 Amortized Distributional Projection Optimization

Amortized optimization often leads to sub-optimality. Hence, it loses the metricity property since the Max-SW only obtains the identity of indiscernibles at the global optimum. Therefore, we propose to predict an entire distribution over projecting directions.

(6) $\begin{equation*} \min_{\phi \in \Phi,\gamma \in \Gamma}\max_{ \psi \in \Psi}\mathbb{E}_{X \sim p(X)} \Big(\mathbb{E}_{\theta \sim \text{vMF}(\epsilon_{\psi,\gamma,\phi},\kappa)} W_p^p(\theta \sharp P_X,\theta \sharp P_{g_\gamma (f_\phi(X))})\Big)^{\frac{1}{p}}, \end{equation*}$

where $\epsilon_{\psi,\gamma,\phi} = a_\psi(X,g_\gamma (f_\phi(X)))$ , $\text{vMF}(\epsilon,\kappa)$ is the von Mises Fisher distribution with the mean location parameter $\epsilon \in \mathbb{S}^{d-1}$ and the concentration parameter $\kappa > 0$ , and

(7) $\begin{equation*} \text{v-DSW}_p(\mu,\nu;\kappa) =\max_{\epsilon \in \mathbb{S}^{d-1}} \Big(\mathbb{E}_{\theta \sim \text{vMF}(\epsilon,\kappa)} \text{W}_p^p(\theta \sharp \mu,\theta \sharp \nu) \Big)^{\frac{1}{p}} \end{equation*}$

is the von Mises-Fisher distributional sliced Wasserstein distance.

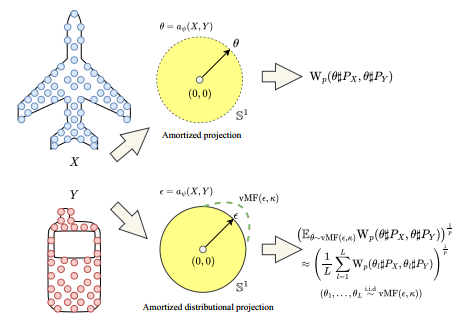
Figure 2. The difference between amortized projection optimization and amortized distributional projection optimization.

3.2 Self-Attention Amortized Models

Based on the self-attention mechanism, we introduce the self-attention amortized model which is permutation invariant and symmetric. Given $X,Y \in \mathbb{R}^{dm}$ , the self-attention amortized model is defined as:

(8) $\begin{equation*} a_\psi (X,Y)=\frac{\mathcal{A}_{\zeta}(X'^\top)^\top \boldsymbol{1}_{m} + \mathcal{A}_{\zeta}(Y'^\top)^\top \boldsymbol{1}_{m}}{||\mathcal{A}_{\zeta}(X'^\top)^\top \boldsymbol{1}_{m} + \mathcal{A}_{\zeta}(Y'^\top)^\top \boldsymbol{1}_{m}||_2}, \end{equation*}$

where $X'$ and $Y'$ are matrices of size $d\times m$ that are reshaped from the concatenated vectors $X$ and $Y$ of size $dm$ , $\boldsymbol{1}_{m}$ is the $m$ -dimensional vector whose all entries are $1$ , and $\mathcal{A}_{\zeta}(\cdot)$ is linear (efficient) attention module [5, 6] for preserving near-linear complexity.

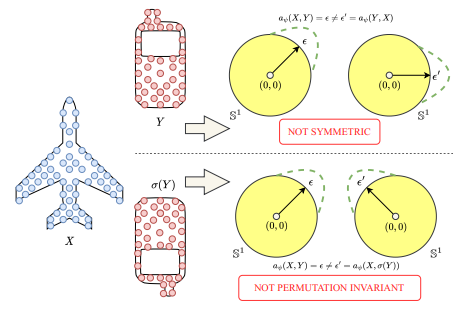
Figure 3. Visualization of an amortized model that is not symmetric and permutation invariant in two dimensions.

4. Experiments

To verify the effectiveness of our proposal, we evaluate our methods on the point-cloud reconstruction task and its two downstream tasks including transfer learning and point-cloud generation (please see our papers for more details).

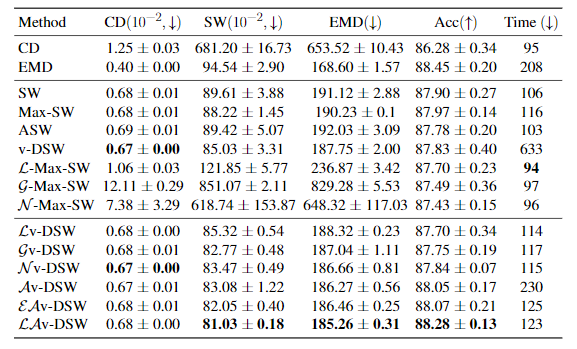
Table 1. Reconstruction and transfer learning performance on the ModelNet40 dataset. CD and SW are multiplied by 100.

Figure 4. Qualitative results of reconstructing point-clouds in the ShapeNet Core-55 dataset. From top to bottom, the point-clouds are input, SW, Max-SW, v-DSW, and $\mathcal{L}\mathcal{A}$ v-DSW respectively.

5. Conclusion

In this paper, we have proposed a self-attention amortized distributional projection optimization framework which uses a self-attention amortized model to predict the best discriminative distribution over projecting direction for each pair of probability measures. The efficient self-attention mechanism helps to inject the geometric inductive biases which are permutation invariance and symmetry into the amortized model while remaining fast computation. Furthermore, the amortized distribution projection optimization framework guarantees the metricity for all pairs of probability measures while the amortization gap still exists. On the experimental side, we compare the new proposed framework to the conventional amortized projection optimization framework and other widely-used distances in the point-cloud reconstruction application and its two downstream tasks including transfer learning and point-cloud generation to show the superior performance of the proposed framework. For further information, please refer to our work at https://proceedings.mlr.press/v202/nguyen23e/nguyen23e.pdf.

6. References

[1] Nguyen, T., Pham, Q.-H., Le, T., Pham, T., Ho, N., and Hua,B.-S. Point-set distances for learning representations of 3d point clouds. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), 2021.

[2] Naderializadeh, N., Comer, J., Andrews, R., Hoffmann, H., and Kolouri, S. Pooling by sliced-Wasserstein embedding. Advances in Neural Information Processing Systems, 34, 2021.

[3] Deshpande, I., Hu, Y.-T., Sun, R., Pyrros, A., Siddiqui, N., Koyejo, S., Zhao, Z., Forsyth, D., and Schwing, A. G. Max-sliced Wasserstein distance and its use for GANs. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 10648–10656, 2019.

[4] Nguyen, K. and Ho, N. Amortized projection optimization for sliced Wasserstein generative models. Advances in Neural Information Processing Systems, 2022.

[5] Shen, Z., Zhang, M., Zhao, H., Yi, S., and Li, H. Efficient attention: Attention with linear complexities. In Proceedings of the IEEE/CVF winter conference on applications of computer vision, pp. 3531–3539, 2021.

[6] Wang, S., Li, B. Z., Khabsa, M., Fang, H., and Ma, H. Linformer: Self-attention with linear complexity. arXiv preprint arXiv:2006.04768, 2020.

Global-Local Regularization Via Distributional Robustness Read Now

Wavelet Diffusion Models are fast and scalable Image Generators Read Now

Back to Technical Blog

Overall

7 minutes

Khai Nguyen (*), Dang Nguyen (*), Nhat Ho