Thanh Van Le, Hao Phung, Thuan Hoang Nguyen, Quan Dao, Ngoc Tran, Anh Tran
Geodesic-Former: a Geodesic-Guided Few-shot 3D Point Cloud Instance Segmenter
1. Introduction
We introduce a new problem in 3D point cloud: few-shot instance segmentation (3DFSIS). Given a few annotated point clouds exemplified a target class, our goal is to segment all instances of this target class in a query point cloud. This problem has a wide range of practical applications where point-wise instance segmentation annotation is prohibitively expensive to collect. To address this problem, we present Geodesic-Former – the first geodesic-guided transformer for 3D point cloud instance segmentation. The key idea is to leverage the geodesic distance to tackle the density imbalance of LiDAR 3D point clouds. To evaluate Geodesic-Former on the new task, we propose new splits of the two common 3D point cloud instance segmentation datasets: ScannetV2 and S3DIS. Geodesic-Former consistently outperforms strong baselines adapted from state-of-the-art 3D point cloud instance segmentation approaches by a significant margin.
2. Method
A. Problem setting
In training, we are provided a sufficiently large training set of base classes , i.e.,
, where
are the 3D point cloud of the scene
and its ground-truth segmentation masks, respectively, and
is the number of training samples. In testing, given
support 3D point cloud scenes
and their ground-truth masks
to define a new target class
, we seek to segment all instances
of the target class in a query scene
. It is worth noting that the target class is different from the base classes, or
. In this paper, we explore two configurations: 1-shot and 5-shot instance segmentation.
B. Baseline method
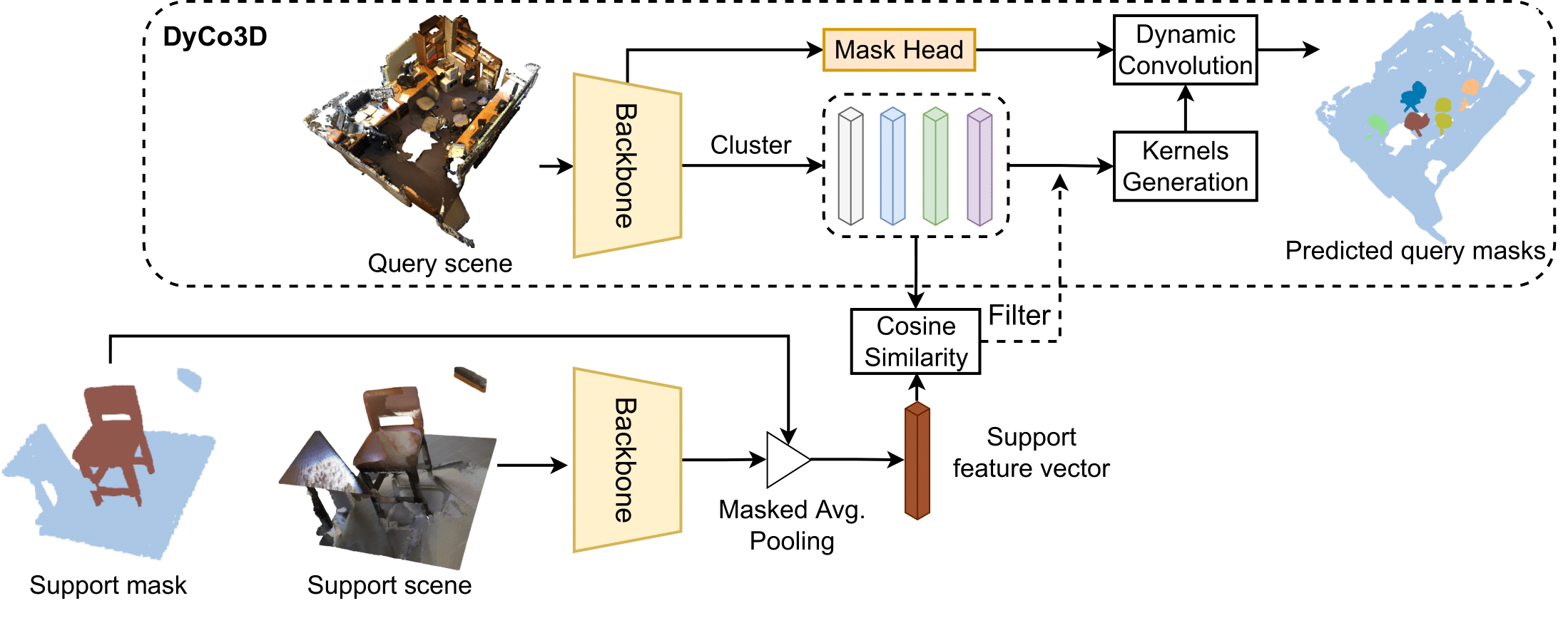
Figure 1: The baseline method of 3DFSIS
A baseline for 3DFSIS can be adapted from a 3D point cloud instance segmenter, e.g., DyCo3D [1], to the few-shot setting. The baseline is depicted in Fig. 1. First, similar points are grouped into candidates based on their Euclidean centroids and semantic predictions. Then each candidate is passed to a subnetwork to generate a kernel for dynamic convolution to obtain the final instance mask. To filter out the irrelevant candidates which do not belong to the target class, one can use cosine similarity between the support feature vector and the average feature vector of all points of each candidate.
This framework has several limitations. First, 3D point clouds are imbalanced in density and mostly distributed near the object surface so that the Euclidean distance for clustering is unreliable, i.e., points that are close together might not necessarily belong to the same object and vice versa. Second, the clustering in DyCo3D relies heavily on the performance of the offset centroid predictions and hence might be overfitting to the particular 3D shape and size of the training object classes, resulting in poor generalization to the test classes.
C. Our proposed method
To address these limitations, we propose a new geodesic-guided transformer decoder to generate the kernel for the dynamic convolution from a set of initial anchor points, giving the name of our approach, Geodesic-Former. The overview of Geodesic-Former is depicted in Fig. 2.
First, geodesic distance embedding based on the geodesic distances between each of the anchor points to all context points is computed. In this way, the geodesic distance between two points belonging to different objects is very large, helping differentiate different objects. To obtain the geodesic distance, we first employ the ball query algorithm [2] to get a directed sparse graph whose nodes are context points and each node only connects to at most other nodes. There exists a directed edge from node 1 to node 2 if node 2 is among the
nearest neighbors of node 1 and within a radius
, and the weight of the edge is always positive and equal to the local Euclidean distance between the two nodes. After that, we use the shortest path algorithm, i.e. Djikstra [3], to compute the length of the shortest path from each anchor point to every context point in the obtained sparse graph as its geodesic distance. Finally, the geodesic distance embedding
of an anchor point
is obtained by encoding its geodesic distance using the sine/cosine function in [4]. Then this embedding is used as positional encoding to guide the later transformer decoder and dynamic convolution.
Second, to avoid overfitting to the shape and size of training classes, we use a combination of the Farthest Point Sampling, a similarity network, and a transformer decoder. The first samples initial seeds from the query point cloud representing the initial locations of the object candidates, the second filters out irrelevant candidates, and the third contextualizes the foreground (FG) candidates to precisely represent objects with the information of the context points to generate the convolution kernels. In this way, as long as an initial seed belongs to an object, it can represent that object. In contrast, for each point, DyCo3D has to predict exactly the center point of the object it belongs to for the clustering to work well. This is even harder when transferring to the new object classes in testing. Also, to the best of our knowledge, we are the first to adopt the transformer decoder architecture to the 3DIS and 3DFSIS.
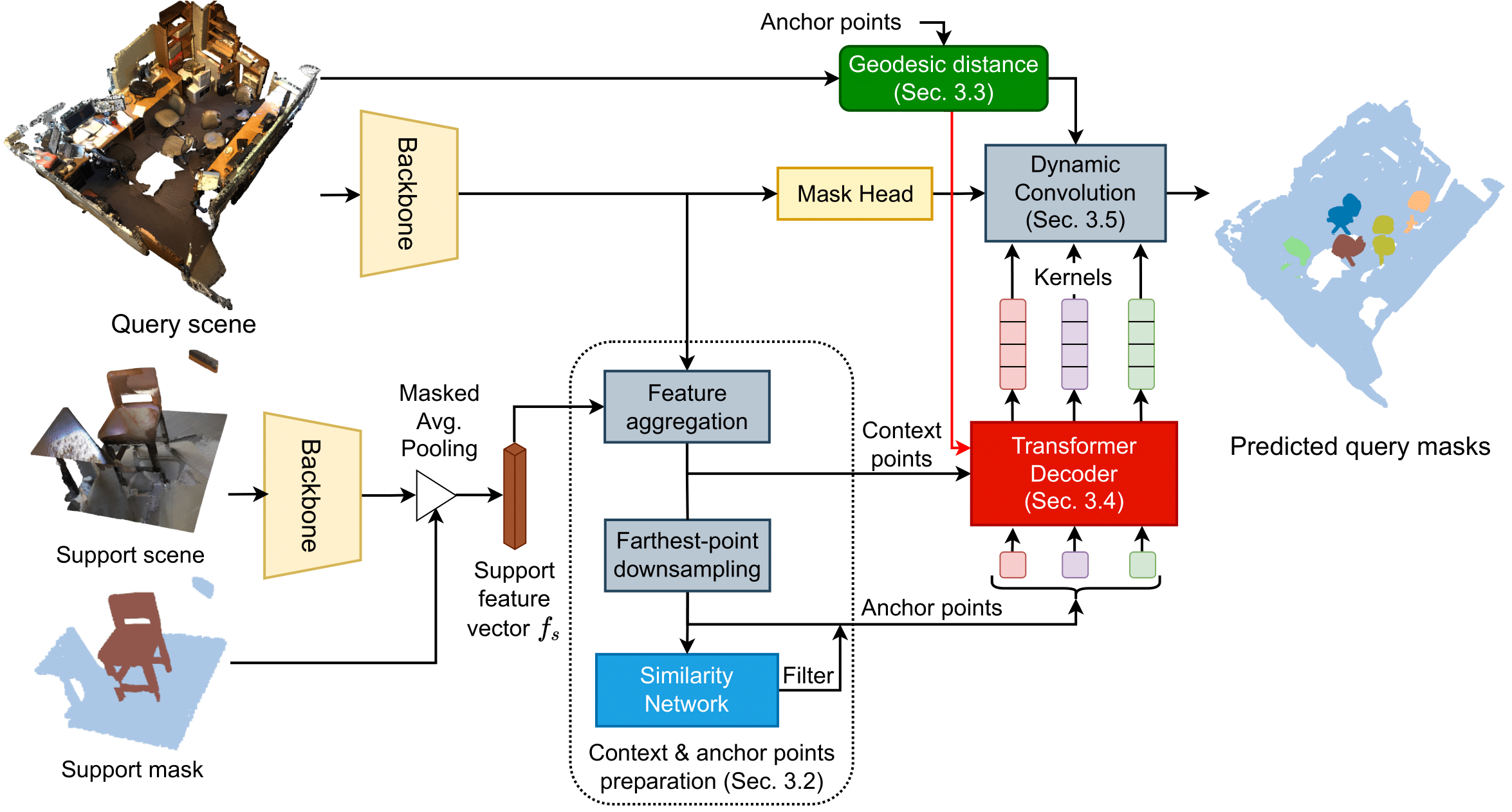
Figure 2: Our proposed approach, Geodesic-Former for 3DFSIS
D. Training Strategy
Pretraining:
First, we pretrain the backbone, mask head, and transformer decoder with the standard 3D point cloud instance segmentation task on the base classes. In this stage, the feature aggregation in Fig. 2 is not used since we do not have support feature, instead, we copy the features of query points to the context points directly. Also, we add a classification head on top of the output of the transformer decoder to predict the semantic category along with the kernel generation to predict the mask for each anchor point.
Episodic training:
We leverage the episodic training strategy to mimic the test scenario in training. That is, for each episode, we randomly sample a pair of support and query point clouds and their masks from training examples of the base classes. In this stage, the classification head is removed, and we add feature aggregation and similarity network to train with the transformer decoder while freezing the backbone and mask head.
3. Experiments
A. Datasets
To evaluate Geodesic-Former on the new 3DFSIS task, we introduce two new datasets derived from ScannetV2 [4] and S3DIS [5] used for 3D point cloud instance segmentation.
- ScannetV2 consists of 1613 point clouds of scans with 20 semantic classes in total and 18 classes for instance segmentation. We split the 18 foreground classes into two non-overlapping folds with nine classes each, one for training classes (fold 0) and the other for test classes (fold 1).
- S3DIS contains 272 point clouds collected from 6 large-scale areas with 13 semantic categories. We only keep 12 main categories and remove the “clutter” class. We also split it into two folds with six classes each. Tab. 1 summarizes the class splits of ScannetV2 and S3DIS.
B. Evaluation metrics
For ScannetV2, we adopt the mean average precision (mAP) and AP50 used in the instance segmentation task. For S3DIS, we apply the metrics that are used in [1] to test classes: mCov, mPrec, and mRec. They are the mean instance-wise IoU, mean precision, and mean recall.
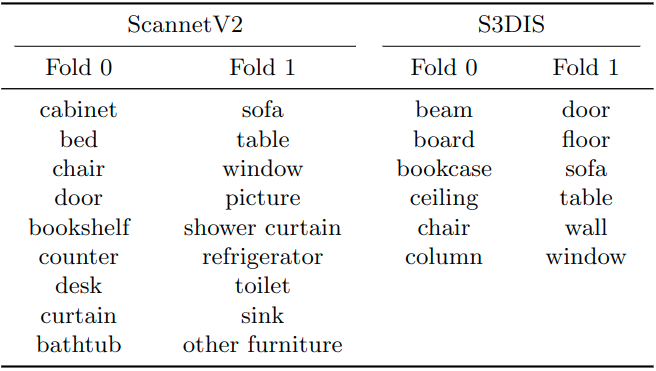
Table 1: Class splits of the ScannetV2 and S3DIS datasets.
C. Comparison with Prior Work
Since there is no prior work on 3DFSIS, we adapt three state-of-the-art (SOTA) approaches on 3DIS: DyCo3D [1], PointGroup [6], and HAIS [7] to the few-shot setting for comparison with our approach. Table 2 and Table 3 show the comparison results on the S3DIS and ScannetV2 datasets, respectively. Geodesic-Former consistently outperforms all of them by a large margin in all metrics, i.e., +4.4 for one shot and +6.8 for five shots in the mAP. Moreover, our method is more robust across different runs where the standard variations of mAP and AP50 are only 0.7 and 1.4, respectively, compared with 2.0 and 3.1 of the second-best DyCo3D’s.
For S3DIS, our method outperforms others by a significant margin, i.e., in mCov and mRec, about +4 for one shot and +7 for five shots. HAIS’s results are slightly better than ours in mPre due to its strict threshold to get high precision but low recall rate.
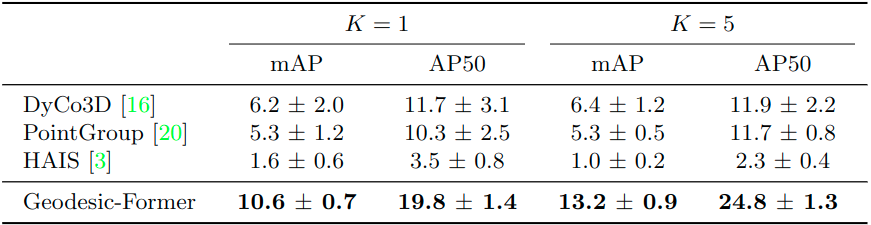
Table 2: Comparison of Geodesic-Former and other baselines on ScannetV2.
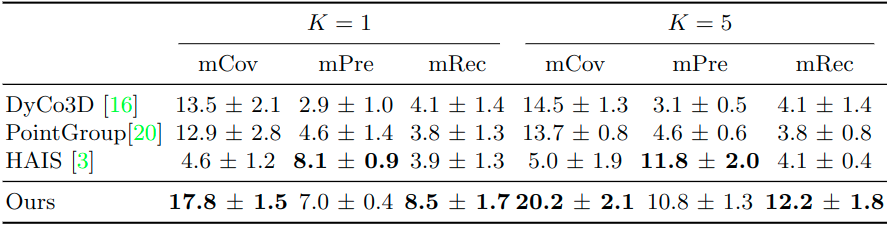
Table 3: Comparison of Geodesic-Former and other baselines on S3DIS
D. Ablation Study
Similarity network, transformer decoder, geodesic distance: In Table 4, the first and second rows show the performance of our baseline in Figure 1 and a per-point classification variant where we use cosine similarity to filter out irrelevant points before clustering by predicted objects’ centers. This variant performs poorly as each point is classified independently without geometric cues of objects, and the classified points are so cluttered to form a complete shape. When replacing the cosine similarity in the baseline with a similarity network, the performance slightly increases, +0.4 in row 3. When the transformer decoder replaces the clustering algorithm in the baseline, the performance also slightly improves, +0.5 in row 4. Especially when adding the geodesic distance embedding to the dynamic convolution of the baseline, the performance is significantly boosted, +1.6 in row 5. Finally, our full approach achieves the best performance, 10.6 in mAP and 19.8 in AP50.
Number of anchor points: In Figure 3, using the number of anchor points of 128 gives the best results. This is because using too few anchor points cannot capture the diversity of objects in the scene, whereas using too many does not boost performance significantly.
E. Qualitative Results
Figure 4 shows the qualitative results of our approach and others on ScannetV2. For the training class “chair” shown on row 1, all approaches perform well. For the test classes (rows 2-5), there are differences in the segmentation results. These examples demonstrate the strong capability of our approach when handling objects to various extents thanks to the transformer decoder and the geodesic distance embedding. However, our method mis-segments the sofa-stool as a sofa due to their similar appearance (row 5).
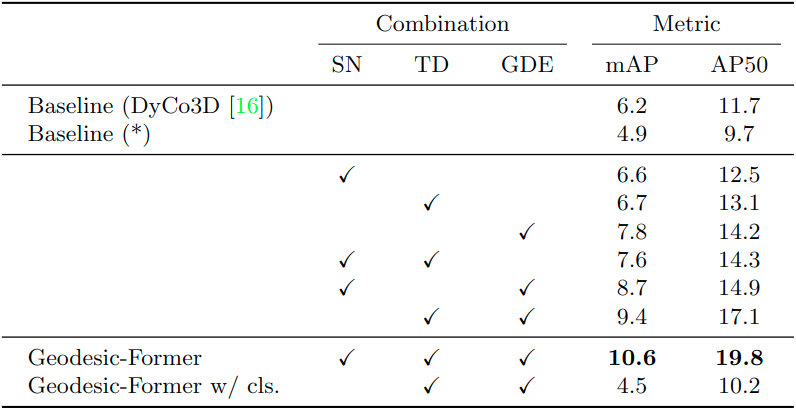
Table 4: Ablation study on each component’s contribution to the final results.
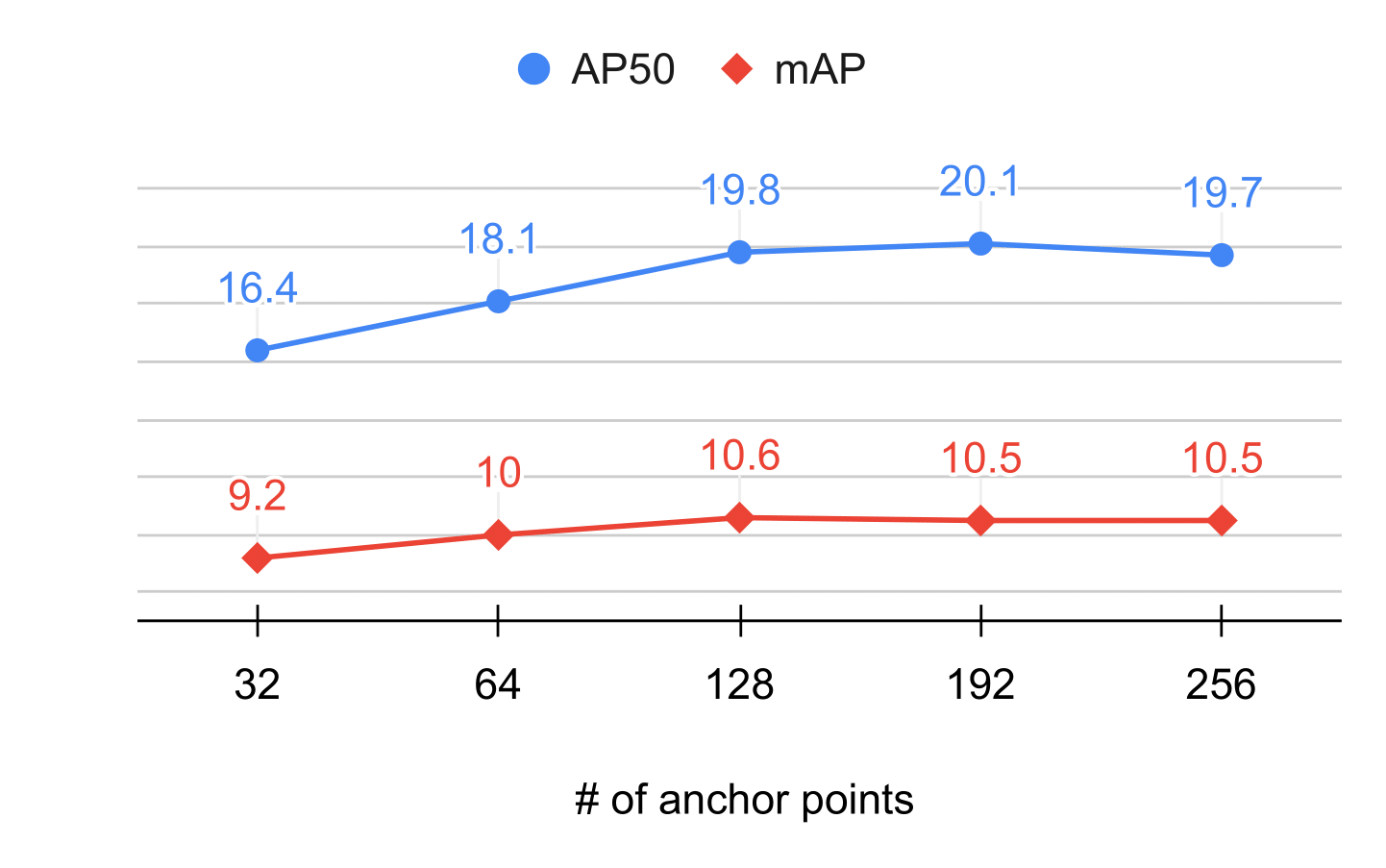
Figure 3: Study on the number of anchor points.
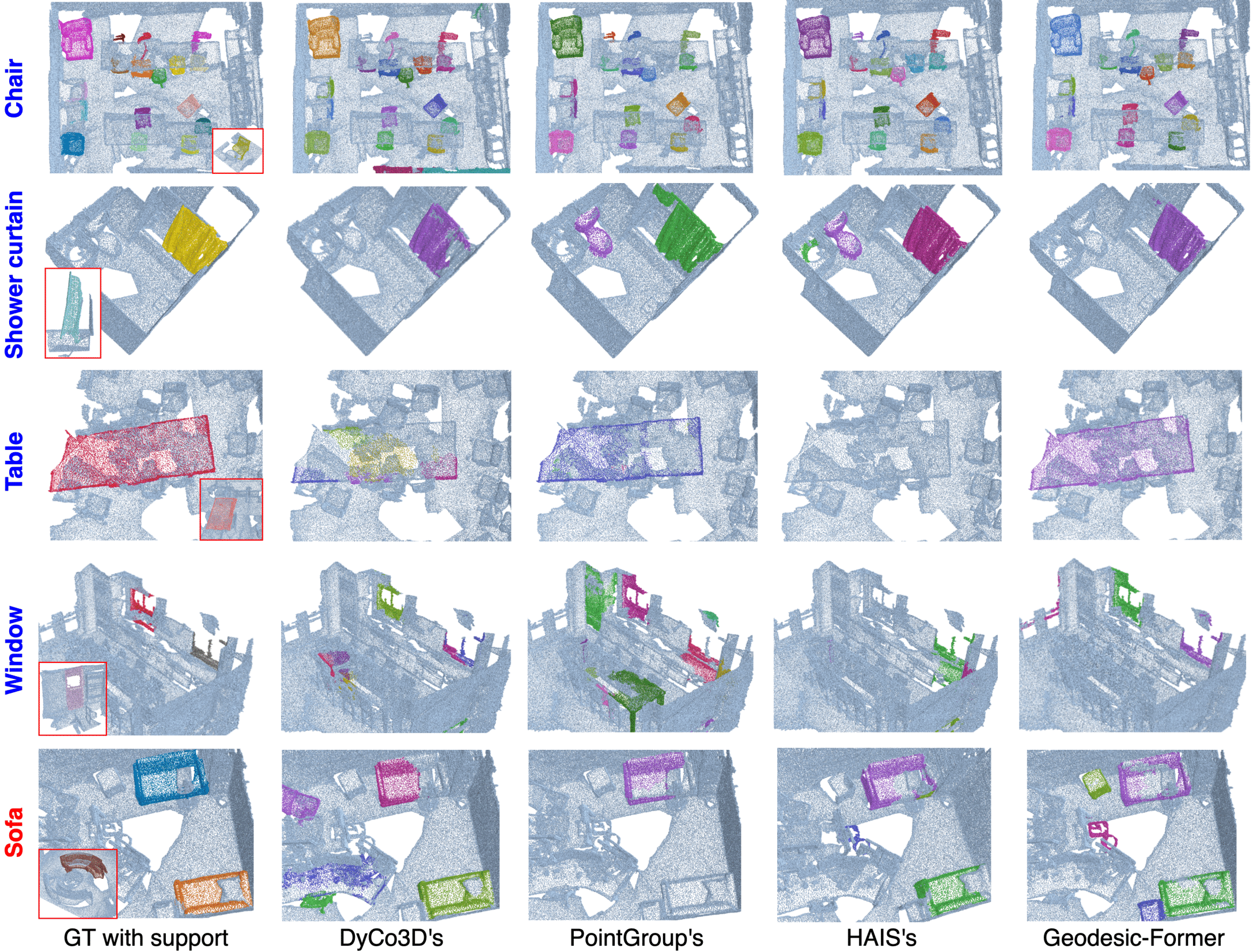
Figure 4: Qualitative results of Geodesic-Former and other baselines on the ScannetV2.
4. Conclusion
In this work, we have introduced the new few-shot 3D point cloud instance segmentation task and have proposed the Geodesic-Former – a new geodesic-guided transformer with dynamic convolution to address it. Extensive experiments have been conducted on the newly introduced splits of ScannetV2 and S3DIS datasets showing that our approach achieves robust and significant performance gain on both datasets from the very strong baselines adapted from the state-of-the-art approaches in 3D instance segmentation.
5. References
[1] He, Tong, Chunhua Shen, and Anton van den Hengel. “Dyco3d: Robust instance segmentation of 3d point clouds through dynamic convolution.” Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2021.
[2] Qi, Charles R., et al. “Pointnet: Deep learning on point sets for 3d classification and segmentation.” Proceedings of the IEEE conference on computer vision and pattern recognition. 2017.
[3] Dijkstra, Edsger W. “A note on two problems in connexion with graphs.” Edsger Wybe Dijkstra: His Life, Work, and Legacy. 2022. 287-290.
[4] Dai, Angela, et al. “Scannet: Richly-annotated 3d reconstructions of indoor scenes.” Proceedings of the IEEE conference on computer vision and pattern recognition. 2017.
[5] Armeni, Iro, et al. “3d semantic parsing of large-scale indoor spaces.” Proceedings of the IEEE conference on computer vision and pattern recognition. 2016.
[6] Jiang, Li, et al. “Pointgroup: Dual-set point grouping for 3d instance segmentation.” Proceedings of the IEEE/CVF conference on computer vision and Pattern recognition. 2020.
[7] Chen, Shaoyu, et al. “Hierarchical aggregation for 3d instance segmentation.” Proceedings of the IEEE/CVF International Conference on Computer Vision. 2021.
Overall
Tuan Ngo and Khoi Nguyen
Share Article




